No właśnie. Co to jest? Co to za ustrojstwo? Wbrew pozorom sama idea nawigacji bezwładnościowej nie jest skomplikowana. Poniższy film przedstawia przykład implementacji tego cuda.

Bezwładność

Zacznijmy od magicznego słowa „bezwładnościowa”. Każdy z nas czuł na własnej skórze siłę bezwładności podczas ruszania i hamowania samochodem. Pochodzi ona od działających na nas przyspieszeń i naszej masy.

$$ F_b = a \cdot m $$

Wynika z tego, że przyspieszenie można policzyć znając masę i siłę bezwładności.

$$ a = \frac{F_b}{m} $$

Powyższa zależność jest wykorzystywana do wyznaczania przyspieszeń przez różnego rodzaju akcelerometry, które to właśnie mamy w swoich telefonach. Łatwizna.

Jeśli chcesz zgłębić temat siły bezwładności polecam ten artykuł.

Ale gdzie tu ta nawigacja?

System nawigacji ma nam dawać informację o naszym położeniu. Ale jak sprawdzić swoją pozycję na podstawie przyspieszeń? Znów muszę odwołać się do tej brzydkiej i złej mechaniki:

$$ \iint_{0}^{t} a(t) = s(t) $$

Jeśli ktoś właśnie zzieleniał na widok powyższego równania i chce wyłączyć tego posta to uspakajam. Nie ma się czego bać! Równanie to mówi nam tyle, że w celu obliczenia przemieszczenia obiektu wystarczy dwa razy scałkować działające na niego przyspieszenia. To na prawdę banalne zadanie. Uwierz mi.

Całkowanie numeryczne

Całka z danej funkcji to w uproszczeniu pole pod jej wykresem. Obliczenie tego pola dla funkcji zarejestrowanych przyspieszeń w czasie będzie realizowane metodą trapezów. Wygląda to mniej więcej tak:

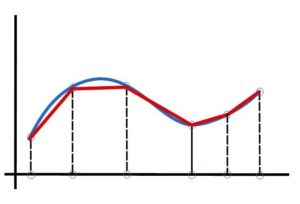
Niebieska linia to przebieg całkowanej funkcji a czerwona jest jej przybliżeniem. Jak widać pole pod wykresem zostało przybliżone do pięciu trapezów a obliczenie ich pól jest już łatwym zadaniem. Im więcej trapezów użyjemy do przybliżenia tym będzie ono dokładniejsze. Nie takie straszne, prawda?

Tutaj znajdziesz przykład takiego całkowania krok po kroku.

Podsumowanie

W najbliższym czasie zbadam dokładność czujników w moim telefonie i sprawdzę czy projekt w ogóle ma sens. Mam nadzieję, że moje obawy co do ich jakości się nie potwierdzą. Stay tuned!